Suppose we wanted the following code instead. What condition would have to be used in the if statement? We want the same result as before, but the if statement is to be constructed differently. if (________________) rate = 0.7; else rate = 0.8; Now draw a flowchart that will include the two types of customers. First test if t == 'r'. For both the true (residential) and the false (commercial) side of that condition, we must add the units condition of u <= 200? Lastly use the Table to determine the rates for each of the four instances. 

Next, convert the flowchart into code. A sample program is listed on the right.
| if ( u > 200) rate = 0.7; else rate = 0.8; #include <stdio.h> int main(void) { int u = 0; char prop_type; double rate; printf("Enter the property type: r-residential, c- commercial: \n"); scanf_s(" %c", &prop_type, sizeof(char)); printf("Enter the unit used: \n"); scanf_s("%d", &u, sizeof(int)); if(prop_type == 'r') { if (u > 200) { rate = 0.7; printf("Your rate is %.2f\n", rate); } else { rate = 0.8; printf("Your rate is %.2f\n", rate); } } if(prop_type == 'c') { if (u > 200) { rate = 0.3; printf("Your rate is %.2f\n", rate); } else { rate = 0.6; printf("Your rate is %.2f\n", rate); } } return 0; }




|
| | |
Now draw a flowchart for the same logic, but instead of dividing the logic first by the type of customer, divide it first by the units consumed. Start with u <= 200, then on both sides of the flowchart test for t == 'r'. Complete the flowchart and write the code for the flowchart. 

| #include <stdio.h> int main(void) { int u = 0; char prop_type; double rate; printf("Enter the unit used: \n"); scanf_s("%d", &u, sizeof(int)); printf("Enter the property type: r-residential, c-commercial: \n"); scanf_s(" %c", &prop_type, sizeof(char)); if(u > 200) { // take note the uses of == instead of = if (prop_type == 'r') { rate = 0.7; printf("Your residential rate is %.2f\n", rate); } else { rate = 0.3; printf("Your commercial rate is %.2f\n", rate); } } else { if (prop_type == 'r') { rate = 0.8; printf("Your residential rate is %.2f\n", rate); } else { rate = 0.6; printf("Your commercial rate is %.2f\n", rate); } } return 0; }
A sample input and output shown below.
|
|
| | |
We will read in three integers:a,b and c. We want to construct the logic so that, no matter how these numbers were provided by the user, the output will always be the three numbers printed in order. For example, if we read in 40, 20,60 into a,b and c respectively, then our logic would print b,a and c in that order. This will give an output of 20,40 and 60. Or if we read in 70, 10 and 60, then the output would beb, c and a in that order. This will give an output of 10, 60 and 70.
If a is greater thanb and b is greater than c, isa greater thanc? Is there any variable that we can say is the largest? Is there any variable that we can say is the smallest? If a is greater thanb and c is greater than b, isa greater thanc? Is there any variable that we can say is the largest? Is there any variable that we can say is the smallest?
| Yes. a > b, b > c so a > c. Yes, there are. Yes, there are. May be or may be not. The possibilities are a > c, a < c or a == c. May be or may be not. Yes.
|
| | |
Some part of the solution will be done for you and please study it carefully. To begin developing this logic, draw a partial flowchart that starts with the comparison of a > b?. On its true side, there is another decision diamond that comparesb > c? Also, print the order of the three variables for the case when it can be determined. 
|
| | |
If a is greater than b and b is greater than c, then we know that a is the largest, followed by b and last by c. On the false side of b > c?, which variable do we know for sure is the largest or the smallest? Add an appropriate diamond there and show a printf() on both sides of the diamond. On the false side of b > c?, we know that a is greater than b and c is greater than (or equal to) b. Since b is the smallest, we need a diamond to determine the relationship between a and c. On the false side of that diamond,c is the largest, a is next and b is the smallest. On the true side of it, we have the same order, but the a and c are switched. 
|
| | |
On the false side of a > b?, add a diamond that checks b > c?. Then show one printf() on the correct side of the diamond that prints the variables in order without requiring an additional diamond. 
|
| | |
Finally, complete the flowchart by adding an a > c? diamond on the true side. 
|
| | |
If a = 5,b = 10 and c = 3, through how many decisions would the logic flow? Convert this into code snippet.
| a > b? is false, b > c? is true and a > c? is true. So the answer is 3. From the flowchart we can build a code snippet as shown below.
if(a < b) if(b > c) printf("The result: %d %d %d\n", a, b, c); else if(a > c) printf("The result: %d %d %d\n", a, c, b); else printf("The result: %d %d %d\n", c, a, b); else if(b > c) if(a > c) printf("The result: %d %d %d\n", b, a, c); else printf("The result: %d %d %d\n", b, c, a); else printf("The result: %d %d %d\n", c, b, a); |
| | |
Let us reconstruct the same logic differently. For the first diamond, use a > c?. For both sides of that diamond, add an a > b? diamond. Show two places where the order of the variables can be determined without requiring any other decision diamonds. So, if a is greater than c and b is greater than a, then we know that b is the largest and c is smallest. On the left side of the flowchart, c is greater than a and a is greater than b, hence, the order of the variables is c, a, b. A portion of the flowchart is shown below.

|
| | |
Add b > c? at two places in the flowchart and complete it. 
|
| | |
| |
The following data are six sets of values of a,b and c. For each problem, label the value of each decision (true, false or N/A). Also, write the order of the variables as they will be printed. The first one is done for you. You may want to refer to the Tutorial in Module 3 for related information.
Problem | a | b | c | a > c | a > b | b > c | Variables’ order | 1 | 4 | 1 | 5 | F | T | F | c, a, b | 2 | 8 | 6 | 5 | | | | | 3 | 2 | 7 | 1 | | | | | 4 | 5 | 2 | 4 | | | | | 5 | 3 | 8 | 9 | | | | | 6 | 5 | 8 | 6 | | | | | Table 4 |
| Problem | a | b | c | a > c | a > b | b > c | Variables’ order | 1 | 4 | 1 | 5 | F | T | F | c, a, b | 2 | 8 | 6 | 5 | T | T | T | a, b, c | 3 | 2 | 7 | 1 | T | F | T | b, a, c | 4 | 5 | 2 | 4 | T | T | F | a, c, b | 5 | 3 | 8 | 9 | F | F | F | c, b, a | 6 | 5 | 8 | 6 | F | F | T | b, c, a | Table 4 |
|
| | |
Next, let us combine conditions by using the logical AND,OR and NOT operators. The operator for AND is &&, for OR is || and for NOT is ! For example, (x == 1) || (x == 2) is true only if x is equal to 1 or 2. Likewise, the expression (x == 1) && (y == 3) is true only if x is equal to 1 and y is equal to 3. Complete the following chart. Notice that when one condition is false and the other is true, the result of ANDing them becomes false because both conditions must be true for the result to be true. However, when ORing them, only one has to be true for the outcome to be true.
Condition1 | Condition2 | Condition1 &&Condition2 | Condition1 ||Condition2 | F | F | | | F | T | F | T | T | F | | | T | T | | | Table 5 |
| Condition1 | Condition2 | Condition1 && Condition2 | Condition1 || Condition2 | F | F | F | F | F | T | F | T | T | F | F | T | T | T | T | T | Table 5 |
|
| | |
The condition !(x == 1) is true as long as x is not equal to 1. The ! reverses the logic. It can also be expressed as x != 1. If a condition is true, then NOT’ing it makes it false and if it is false, then NOT’ing it makes it true. Similar to the table above, show the two-entry table for Condition1, which has the values of F and T, and the NOT of Condition1.
Condition1 | !Condition1 | T | | F | | Table 6 |
| Condition1 | !Condition1 | T | F | F | T | Table 6 |
|
|
Complete the truth table for this chart and combine the three kinds of logic. Find the NOTs of both conditions and then AND them.
Cond1 | Cond2 | !Cond1 | !Cond2 | (!Cond1) && (!Cond2) | F | F | | | | F | T | T | F | F | T | F | | | | T | T | | | | Table 7 |
| Cond1 | Cond2 | !Cond1 | !Cond2 | (!Cond1) &&(!Cond2) | F | F | T | T | T | F | T | T | F | F | T | F | F | T | F | T | T | F | F | F | Table 7 |
|
| | |
Complete the following chart and state whether (!Cond1) && (!Cond2) is equivalent to !(Cond1 || Cond2).
Cond1 | Cond2 | Cond1 || Cond2 | !(Cond1 || Cond2) | F | F | | | F | T | T | F | T | F | | | T | T | | | Table 8 |
| Cond1 | Cond2 | Cond1 ||Cond2 | !(Cond1 ||Cond2) | F | F | F | T | F | T | T | F | T | F | T | F | T | T | T | F | Table 8 |
|
| | |
In all the previous C codes, there is no error checking implemented. For example, we declared int variable but what happen if users key-in a character? What happen if the Operating System itself having problem? In the real programming world we need to provide the exit ‘door’ or path for the program if something wrong happens. The simplest one may just quitting the program and exiting or passing to the Operating System by using exit() or terminate() functions. A better method may useException Handling. The best method may use standard and customized error codes and their respective messages combined with exception handling that will provide meaningful information for troubleshooting. When you compile/build your program and there are errors, make sure you correct the first error occurred. For example, compile the following program example.
|
| | |
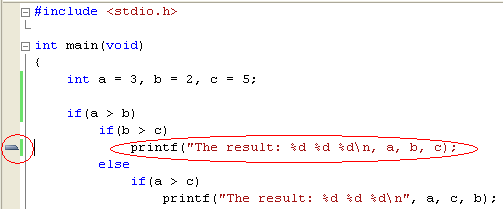
#include<stdio.h> int main(void) { int a = 3, b = 2, c = 5; if(a > b) if(b > c) printf("The result: %d %d %d\n, a, b, c); else if(a > c) printf("The result: %d %d %d\n", a, c, b); else printf("The result: %d %d %d\n", c, a, b); else if(b > c) if(a > c) printf("The result: %d %d %d\n", b, a, c); else printf("The result: %d %d %d\n", b, c, a); else printf("The result: %d %d %d\n", c, b, a); return 0; }
| |
| | |

|
| | |
A pointer on the left (red circle) point to the line that compiler suspected having an error. When we closely check the line we found a missing double quote after the \n. Correct the error and rebuild the program. Well, you can see that there is no more second error. That is why we need to correct the first error occurred and when we already corrected the first error, continue rebuilding/recompiling the program instead of correcting the next error. If you cannot find the error(s) in the pointed line, please check the lines of code before the pointed line. That is a normal location where the errors occurred.
|



















